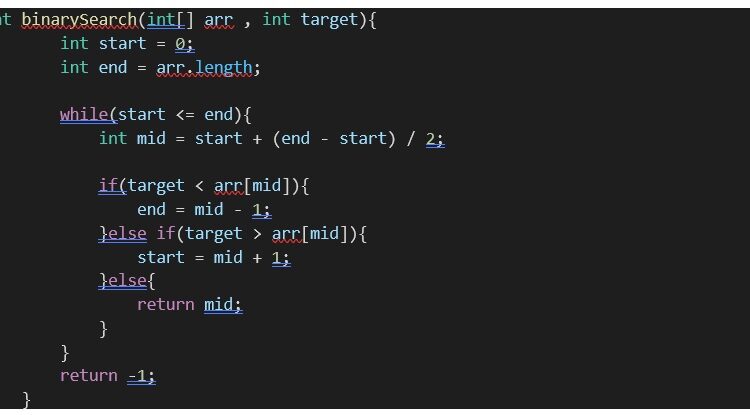
Given in an array of functions that you need to write to use linear search in Java. Following is the algorithm that should be followed.
Algorithm:
Stage 1: Start
Stage 2: Declare an array and search component as a key.
Stage 3: Traverse the exhibit until the number is found.
Stage 4: If the key component is found, return the record position of the exhibit component
Stage 5: If the key component isn’t found, return – 1
Stage 6: Stop.
Procedure
Technique Linear search( list, value)
For each item in the list,
If same item= value
Return the location of the item
End if
End for
End procedure
Java
// Java code for straight search x in arr[]. If x
// is available then return its area, in any case
// return – 1
class Linear Search {
// This capability returns list of component x in arr[]
static int search(int arr[], int n, int x)
{ for (int I = 0; I < n; i++) {
// Return the list of the component if the component // is found
if (arr[i] == x)
bring back; }
// return – 1 if the component isn’t found
return – 1;
}
public static void main(String[] args)
{
int[] arr = { 3, 4, 1, 7, 5 };
int n = arr.length;
int x = 4;
int list = search(arr, n, x);
on the off chance that (file == – 1)
System. out.println(“Element is absent in the cluster”);
else
System.out.println(“Element found at position ” + list);
}
}
Yield:
A component found at position 1
Time Complexity :
The Best Case Complexity
In direct pursuit, the best case happens when the hunt component is available in the main area of the exhibit. So the best-case time intricacy of the straight pursuit is o(1).
The best-case time intricacy of the straight pursuit is o(1).
The Moderate Case Complexity
In a straight hunt, a normal case happens when the pursuit component is available at the arbitrary area of the array. So the typical case time intricacy of the direct inquiry is o(1).
The typical case time intricacy of the straight inquiry is o(n).
The Worst Case Complexity
In direct pursuit, the most pessimistic scenario happens when the hunt component is available at the last area of the exhibit So the most pessimistic scenario time intricacy of the straight hunt is o(1).
In the most pessimistic scenario if the pursuit component is absent in the given cluster then we want to cross the whole exhibit to look through the component. So the most pessimistic scenario time intricacy of the straight hunt is o(n).
The most pessimistic scenario time intricacy of the straight hunt is o(n)
The Space Complexity
The space intricacy of the direct pursuit is o(1)
Linear Search in Java Applications
It is used in direct pursuit of the following things:
- for search thing in the more modest exhibit.
- For quick looking
The time intricacy of the above calculation is O(n). Kindly allude total article on Linear Search for additional subtleties.